In Geometry, a Triangle is the most crucial shape, defined as a shut two-dimensional diagram having three angles, three sides and three vertices. In other words, a triangle is a polygon with three sides. The word triangle is drawn from the Latin word ‘triangulus,’ which indicates three-cornered. Let’s learn more about types of triangles.

Throughout the old times, astronomers had created an approach called triangulation to determine the far-off stars’ distances. They measure the range from 2 different areas, then gauge the angle produced by change or parallax created by the observer’s motion between both locations. Then they made use of to use regulation of sines for determining the required range.

Egyptian Pyramids were created around 2900 BC. Its form is, in fact, of the 3D pyramid, which has Triangle faces. It is a wholly engineered version that the lengths and also angles on all sides are the same. Miletus (624 BC– 547 BC), a Greek mathematician, adopted Egypt’s geometry and generated Greece.

Aristarchus (310 BC– 250 BC), a Greek mathematician, has utilized the above method to find the distance between the Planet and the Moon. Eratosthenes (276 BC– 195 BC), once again, used the same way to determine the distance around the surface of Earth (called area).

In this post, we are most likely to review the definition of Triangle, different sorts of Triangle and residential or commercial properties, and the real-life application of Triangle.

What is Triangle?

A triangle is a two-dimensional closed number with three sides. It is a polygon with three edges, three vertices, and three angles, forming a shut representation. We utilize the symbol ∆ to represent a Triangle.

Different Types of Triangles

The kinds of Triangle are categorized based on:

The lengths of their sides

Interior angles

Classification of triangles according to the gauge of interior angles

According to the step of interior angles, Triangle can be classified into three categories:

• Acute-angled
• Obtuse-angled
• Right-angled

Acute triangle

A severe angle Triangle is Triangle in which all the three indoor angles are less than 90 degrees.

Every one of the angles a, b as well as c is less than 90 degrees.

Obtuse triangle

An obtuse triangle is a triangle in which among the indoor angles is more than 90 levels.

Angle a is much more obtuse, while angle b and c are acute.

Right-angle Triangle

A right triangle is a triangle in which among the angles is precisely 90 degrees. The hypotenuse is a side of a proper Triangle with the most extended size.

Types of Triangles according to the length of their sides

Triangles can be classified right into three kinds based on the lengths of their sides:

• Scalene
• Isosceles
• Equilateral

Isosceles triangle

An isosceles Triangle is a triangle in which two sides and two angles are equivalent. Equal lengths of a triangle revealed when making an arc on each side.

Equilateral Triangle

An equilateral triangle has all three sides equal and all three interior angles equivalent also. In this case, each indoor angle of an equilateral triangle is 60 levels. An equilateral Triangle is occasionally described as an equiangular triangle since all three angles are equivalent.

In an equilateral Triangle, the sides AB = BC = AC and ∠ ABC =∠ ACB = ∠ BAC

Keep in mind that the angles of an equilateral Triangle do not depend upon the sides’ sizes.

Scalene Triangle

A scalene triangle is Triangle in which all the sides have different steps, and all the interior angles are likewise different.

Properties of Triangle

The properties of Triangle have wide use. Lots of mathematicians used it in solving their problems. Euclidean geometry, as well as trigonometry, make terrific use of buildings of triangles.

Right here are a few standard residential or commercial properties of the triangle:

• A triangle is a 2-D polygon
• A Triangle has three sides, three angles and also three vertices.
• The lengths of any two sides of a triangle are more than the staying side’s size.
• The amount of the lengths of the three sides gives the boundary of a Triangle
• The location of a triangle is equal to the product of the base and the elevation.

Worked examples of different Types of Triangles.

Example 1

Locate the value of angle x in the Triangle listed below.

Solution

This is an isosceles triangle in which two sides are equal, and likewise, two angles are equal. Therefore,

x = (180 °– 70 °)/ 2.

x= 110 °/ 2.

= 55 °.

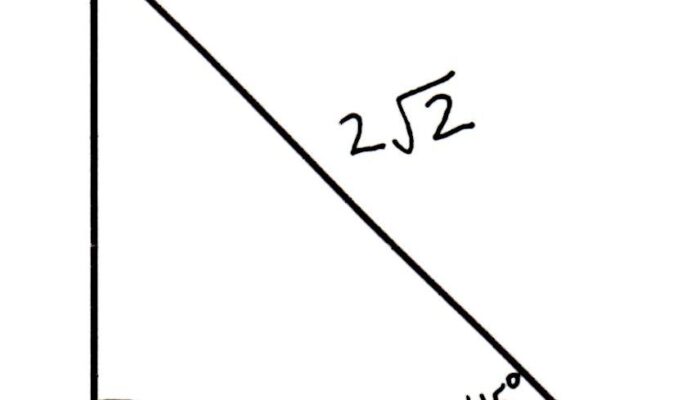
Example 2

Locate angle y in the ideal Triangle revealed below.

Solution

One angle of an ideal triangle is equal to 90 °.

So, we;. y + 50 + 90 = 180.

and, y = (180– 140) °.

y = 40 °.